Dennis Wong home page
Dennis Wong home page

Publications

Gray codes

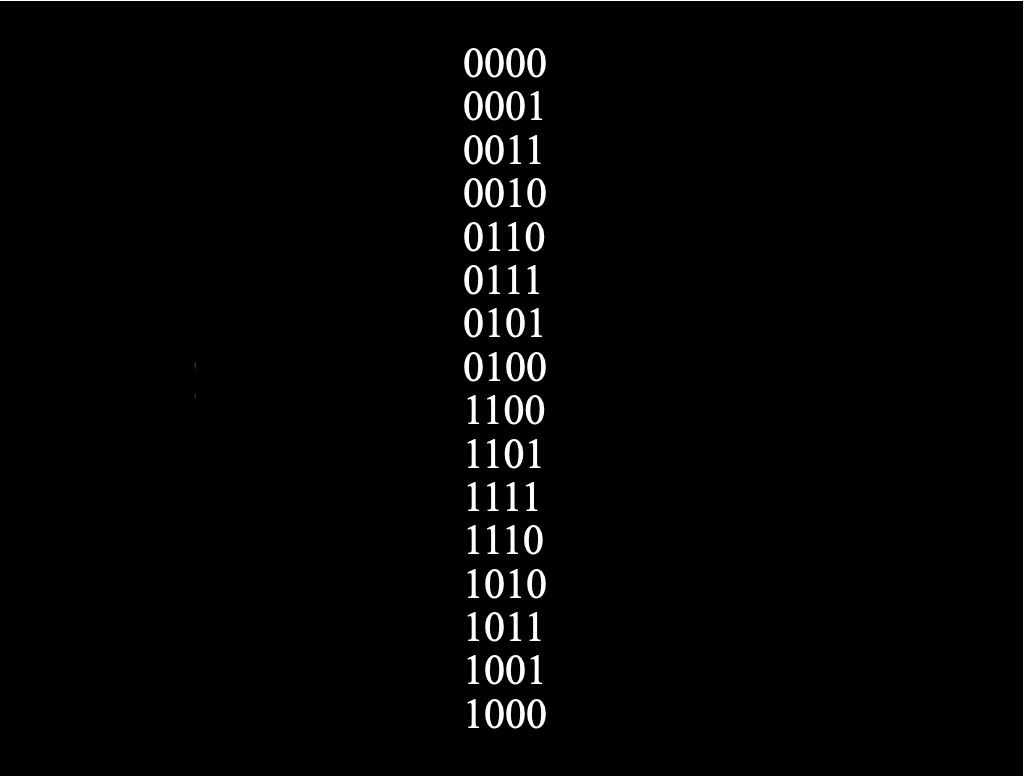
A Gray code for a set S is a listing s1, s2 ,…, s|S| of the elements of S such that consecutive strings in the listing differ by a small amount of changes. As an example, the listing in the figure is a Gray code for the set of length 4 binary strings where consecutive strings differ by exactly one bit. A universal cycle can also be considered as a Gray code, where consecutive strings differ by a single shift and also at most one bit change.

Our goal is to study the existence of Gray codes and devise efficient algorithms to generate Gray codes for various combinatorial objects.

Universal cycles and de Bruijn sequences

A universal cycle for a set S is a cyclic sequence u1u2 … u|S| where each substring of length n corresponds to a unique object in S. As an example, the cyclic sequence in the figure is a universal cycle (de Bruijn sequence) for the set of length 6 binary strings, where the 64 unique length 6 binary strings appear exactly once as a substring when the sequence is considered cyclicly. A universal cycle can also be considered as a Gray code with consecutive strings differ by a shift and at most one symbol change.

Our goal is to study the existence of universal cycle for combinatorial objects, and efficiently construct one if such cycle exists.

Miscellaneous